Gerard J. O'Reilly

Gerard J. O'Reilly

Associate Professor at the Centre for Training and Research on Reduction of Seismic Risk (ROSE Centre) @ IUSS Pavia, Italy

Co-Founder of Djura | Risk - Data - Engineering

Bilinear Demand-Intensity Models

When computing the mean annual frequency of exceedance (MAFE) of a structure limit state using a closed form solution, an expression linking the structural demand to a level of seismic intensity is need. These relationships are termed demand-intensity models and for modern structures with ductile behaviour, these tend to be linear in logspace for deformation-based demands (e.g. storey drift).

However, for other structures with non-ductile behaviour (e.g. infilled RC frames) or strength-related demands (e.g. peak floor acceleration), this demand-intensity model is no longer linear, but rather bilinear. Examples are shown below for the storey drift in an infilled RC frame (below left) and for the peak floor acceleration in a ductile RC frame (below right).

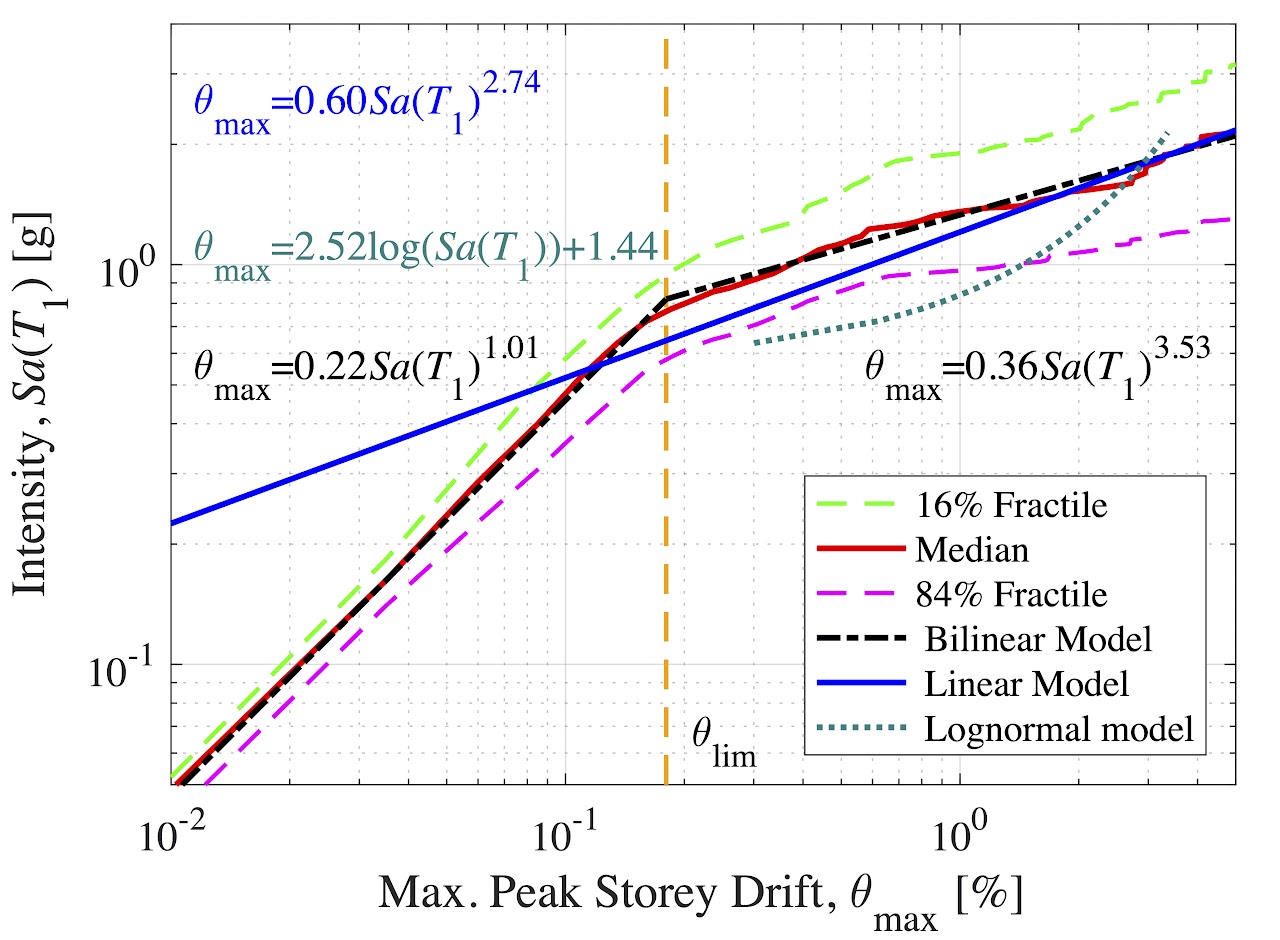
For structures with such a bilinear demand-intensity model, the computation of MAFE requires a reformulation of the mathematical derivation. This has been conducted and implemented into software tools: one a MS Excel sheet and the other a Matlab function. They both perform the same operations to compute the MAFE using the proposed extension described in the references below.

For the latest version of the tool, please visit the Github page here.

Relevant references:

  1. O’Reilly GJ, Calvi GM. Quantifying seismic risk in structures via simplified demand–intensity models. Bulletin of Earthquake Engineering 2020; 18(5): 2003–2022. DOI: 10.1007/s10518-019-00776-0. [PDF][Link]
  2. O’Reilly GJ, Monteiro, R. Probabilistic models for structures with bilinear demand-intensity relationships. Earthquake Engineering and Structural Dynamics 2019; 48 (2): 253-268. DOI: 10.1002/eqe.3135. [PDF][Link]